Thermodynamic Case Study:
Gibbs' Thermodynamic Graphical Method
Envisioning total differentials of scalar functions with two independent variables
as raised surfaces and tangent planes

Objective: To show the independence and sufficiency of a general graphical method coextensive in its application, that when applied to the thermodynamic theory of state demonstrates the relationship between state variables of energy, entropy, volume, temperature, and pressure with and without analytic expressions, where the emphasis will be not to use analytic experssions as recommended by Gibbs and endorsed by Maxwell.

J. Willard Gibbs created the theory associated with thermodynamic state by development of a graphical method in his two historic publications, Part 1, "Graphical Methods in the Thermodynamics of Fluids" and Part 2,"A Method of Geometrical Representation of the Thermodynamic Properties of Substances by Means of Surfaces", Ref.[1]. In the first publication, Part 1, as the title implies, Gibbs developed a general graphical method that provided insight into thermodynamic property relationships governed by the first and second laws of thermodynamics. In the first paragraph Gibbs explains,

"Although geometrical representations of propositions in the thermodynamics of fluids are in general use, and have done good service in disseminating clear notions in this science, yet they have by no means received the extension in respect to variety and generality of which they are capable. So far as regards a general graphical method, which can exhibit at once all the thermodynamic properties of a fluid concerned in reversible processes, and serve alike for the demonstration of general theorems and the numerical solution of particular problems, it is the general if not the universal practice to use diagrams in which the rectilinear co-ordinates represent volume and pressure. The object of this article is to call attention to certain diagrams of different construction, which afford graphical methods coextensive in their applications with that in ordinary use, and preferable to it in many cases in respect of distinctness or of convenience."

Before developing this general graphical method Gibbs combined the equations of the first and second laws into a single equation which to this day is referred to as the Gibbs' equation of state and can be found in any standard thermodynamic textbook.

Figure 1. Gibbs' derivation of the equation of state prior to developing the graphical method, Ref.[1].

The original brief derivation of the equation of state by Gibbs, equation (4), is shown above in Fig. 1. With this derivation Gibbs demonstrates why his "diagrams of different construction" is not just another interesting choice but fundamentally correct in the sense that the first and second laws require that a differential change in energy is related to a corresponding differential change in entropy and volume, not "with that in ordinary use", e.g. pressure and volume. Fundamental indeed. Later in his 1873 publication, Gibbs mentions Thomas Andrews discovery of critical point but does not mention the P-V isotherm diagram Andrew's used in his discusion of critical point. Surely this must have been on Gibbs' mind, but it was not Gibbs style to confront, but rather to note that his diagram was not "with that in ordinary use". Having politely made this point Gibbs continues the development of his graphical method where the focus is now on creating a surface that must be fundmentally related to axes of energy, entropy, and volume, not pressure, volume, and temperature which we continue to use to this day contrary to Gibbs' insightful observation. This significant point provides the insight necessary to understanding Gibbs' lengthy development of his graphical method where ironically only a few figures were actually drawn. The development of the graphical method is accomplished with long descriptive sentences, which are at times difficult to understand. But as we will see, this careful description was necessary if J.C. Maxwell was to reproduce and actually create a three-dimensional (3D) model of Gibbs' fundamental surface in clay and plaster. It was 1873, 3D computer graphics did not exist, however visual thinking within a scientific context requires no such tools or data. After carefully describing various reversible concepts graphically, pp. 310-341, in the next to last paragraph of Ref.[1], part 1, Gibbs concludes,

"In the foregoing discussion, the equations which express the fundamental principles of thermodynamics in an analytical form have been assumed, and the aim has only been to show how the same relations may be expressed geometrically. It would, however, be easy, starting from the first and second laws of thermodynamics as usually enunciated, to arrive at the same results without the aid of analytical formulae, to arrive, for example, at the conception of energy, of entropy, of absolute temperature, in the construction of the diagram without the analytical definitions of these quantities, and to obtain the various properties of the diagram without the analytical expression of the thermodynamic properties which they involve. Such a course would have been better fitted to show the independence and sufficiency of a graphical method, but perhaps less suitable for an examination of the comparative advantages or disadvantages of different graphical methods."

Evidently, according to Gibbs, the equation of state briefly derived at the begining of his first publication was not as insightful as his graphical method. Interesting. To understand how the thermodynamic relationship of properties can be better understood graphically "without the analytic expressions of the various properties" it is necessary to actually read and study Gibbs original 1873 publications, part 1 and 2, Ref.[1]. This emphasis on the graphical method in the first publication (part 1) was further developed in Gibbs' second publication (part 2) as a surface, "A Method of Geometrical Representation of the Thermodynamic Properties of Substances by Means of Surfaces". Using only visual thinking, the relationship between energy, entropy, and volume was envisioned as a surface. After studying Gibbs' publications, James Clerk Maxwell reproduced, in clay and plaster, a sculptured surface of the thermodynamic property relationship that Gibbs envisioned and described in detail but did not draw.

Figure 2. J. Clerk Maxwell sculpture: display case Cavendish Laboratory, Cambridge, England.
Download: http://www-outreach.phy.cam.ac.uk/camphys/museum/area1/images/cabinet1_2.jpg

Maxwell sent one these sculptures to Gibbs (1874), which now gathers dust in a display case at Yale. Another of Maxwell's sculptures can be viewed in a display case at Cavendish Laboratory at Cambridge, Fig. 2. Unlike contemporay ancetodal reports on visual thinking by scientists, Gibbs sufficiently described his visual thinking as a reproducible graphical method. It is important to note that the development of the graphical method has nothing to do with the use of graphical tools. In 1874 there were no graphical tools except for clay and plaster and the sun's grazing rays to locate lines of constant pressure and temperature mapped on the energy-entropy-volume sculptured surface, Refs.[2 and 3]. Maxwell further developed and described how lines of constant temperature and pressure can be scribed on the energy-entropy-volume diagram in his textbook, Theory of Heat, pp. 195-208, Ref.[2]. It is interesting that no equations are used by Maxwell to describe stable and unstable conditions associated with solid, liquid, and gaseous states as well as other state variable relationships. According to Maxwell, the state variable relationships are better understood by using the graphical method as orginially proposed by Gibbs. When the word relationship is used today, it means a mathematical relationship ("formulae"), not in the sense Gibbs and Maxwell envisioned as a graphical method. Because todays reader expects the development of a mathematical derivation not a graphical method, Gibbs' 1873 publication is difficult to understand. This observation is complicated by the fact that Maxwell's diagrams are difficult to envision in 3D. The diagram created by Maxwell, Fig. 3, closely resembles the lines seen on the clay and plaster sculpture in Figure 2. These same lines appear on a postage stamp in honor of Josiah Willard Gibbs, Fig. 4. In fact it is difficult to understand how these lines mapped onto the energy-entropy-volume 3D surface without a picture of the clay and paster model, which was not published with an explanation until 2002, Plates II and III Ref.[3].

Figure 3. Maxwell's graphical model based on Gibbs' original graphical method.
Information highlighted in light blue shows a connection to the equation of state.

Figure 4. Stamp honoring J.W. Gibbs. NOTE: lines of pressure and temperature.

In a letter to Thomas Andrew, 15 July 1875, Ref.[3], Maxwell describes a clever way to draw these lines onto the surface by using parallel rays of light: "When I had at last got a plaster cast I drew on it lines of equal pressure and equal temperature, so as to get a rough notion of their forms. This I did by placing the model in the sun light, and tracing the curve when the rays just grazed the surface. For it v(olume), φ(entropy), and e(nergy) are the co-ordinates, P(ressure) = de/dv, and T(emperature) = de/d(φ)." Of course this is a simple task using current graphical software tools. However the graphical method was developed independent of the tools, e.g. either contemporary computer graphic software or clay and plaster in 1874. Tools are still important, however, the thought behind development of the graphical method occurs first by how the scientist understands the science. It is the intent here to show how Gibbs' energy-entropy-volume sculpture with lines of constant pressure and temperature scribed on the sculptured surface, can be implemented using a general graphical method developed to envision the total differential of any arbitrary scalar function with two independent variables. Such a general graphical method, as it relates to existing analytic methods, is summarized below.

Figure 5. Developement of the graphical method used to understand the total
differential of any arbitrary scalar function of two indenpendent variables.       

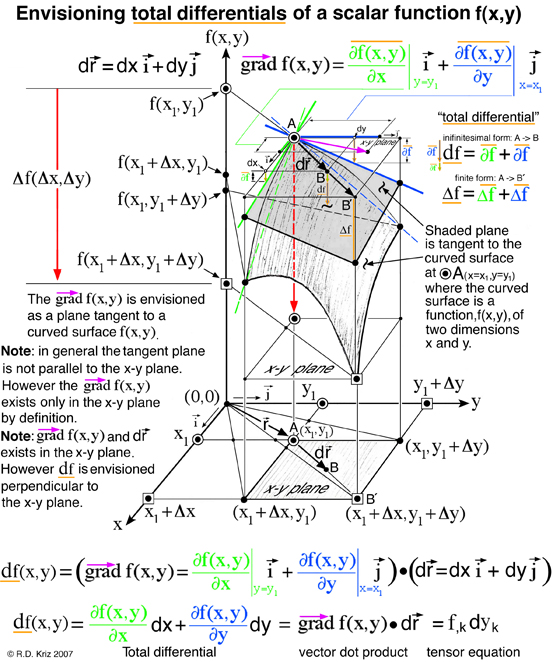
The figure above demonstrates that envisioning the total differential of a scalar function, f(x,y), is an extension of envisioning the gradient of the same scalar function f(x,y) by combining this vector gradient with the inifinitesimal position vector that defines two points, A and B. Mathematically, points A and B coexist in the x-y plane as a vector. However for the thermodynamicists Gibbs and Maxwell, who first envisioned thermodynamic state as a graphical method, each of these points represented a unique thermodynamic state that exist on a curved surface that define three thermodynamic state variables, energy, entropy and volume. Although points A and B coexist in the entropy-volume plane in a mathematical sense, to Gibbs and Maxwell these points are projected upwards onto the energy-entropy-volume surface in a graphical sense. Gibbs discusses this idea in the last paragraph of Ref.[1], part 1,

"The possibility of treating the thermodynamics of fluids by such graphical methods as have been described evidently arises from the fact that the state of the body considered, like the position of a point in a plane, is capable of two and only two independent variations. It is, perhaps, worthy of notice, that when the diagram is only used to demonstrate or illustrate general theorems, it is not necessary, although it may be convenient, to assume any particular method of forming the diagram; it is enough to suppose the different states of the body to be presented continuously by points upon a sheet."

Figure 6. Figures 1, 2, and 3 combined with color as described by Maxwell in Ref.[3].
A poster-sized graphical summary of Gibbs' and Maxwell's figures combined
provides a link to the original graphical thinking developed by Gibbs in Ref.[1].

Although Maxwell carefully defined and constructed lines of constant pressure and temperature, see Fig. 3, there was confusion in understanding how these lines mapped onto the energy-entropy-volume surface. Professor W.P. Boynton and two of his students at the University of California, Berkely, unsuccessfully attempted to recreate Maxwell's sculpture, Ref.[4], from the fig.26d on page 207, Ref.[2]. After reading Boynton's paper it is interesting to observe first hand how important it is to at least have a photograph of Maxwell's sculptured surface. Unless you've visited the display case at the Cavendish Physics Laboratory, only recently (2002) a photograph of Maxwell's clay and plaster model was published, Plates II and III in Ref.[3], as well as posted on the web, see Fig. 2.

Understanding that Gibbs original Fig. 1 is three dimensional is also difficult to see, as shown below, where the entropy and volume axis is not perpendicular. A simple modification is first necessary before projecting this figure into Maxwell's three-dimensional energy, entropy, volume coordinate space. With this modified figure using only visual thinking in a scientific context, pp. 385-388, Gibbs derives a well known relationship called the Clausius-Clapeyron equation by envisioning "... successive positions of the rolling plane ..." that come in contact with the "L" (liquid) and "V" (vapor) tangent points on the "primitive" ("thermodynamic") energy surface where a differential change in the angle of rotation, dθ, about line LV which gives rise to a differential change in slopes for pressure, dp, and temperature, dt, which in turn is used to show dp/dt= BL/CV=Δη/Δυ in Fig.7 below. Using the definition for heat of vaporization, Gibbs recalls Δη = [heat of vaporization, r] / t, hence dp/dt = r / [tΔυ] which is the well know Clausius-Clayperon equation, where Δυ associated with the volumetric expansion as the liquid expands to vapor is the same as the line length CV.

Figure 7. Gibbs' original Figure 1 modified to show 3D axes.

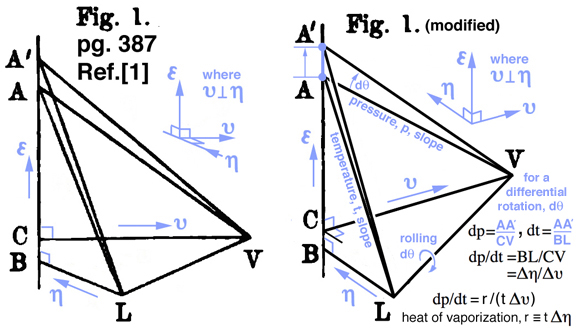
Creating 3D figures was a challenge in 1873. Perhaps this partially explains why the graphical method was not fostered, but the analytical model continued to be developed over the last 134 years. When information in Figures 1, 2, and 3, part 2 of Ref.[1]. is combined with using color originally proposed by Maxwell in Plates IV and V, Ref.[3], it is much easier to understand Gibbs' graphical method. Maxwell explains that the sculpture is a hypothetical model (".. not to scale ..") that communicates the idea of thermodynamic state as a surface that was described by Gibbs in Ref.[1] but not drawn by Gibbs. This emphasis on using the geometric thinking to develop thermodynamic state theory was discussed in Ref.[5], "It is the geometry that led Maxwell into the discussion of the physics, rather than the physics leading to a sense of the surfaces that may represent those properties. Clearly geometry allowed Maxwell to penetrate the physics of thermodynamics in new ways." Although the discussion and development of new physics motivated by geometric thinking is extremely rare, Gibbs' and Maxwell's published results demonstrated it is possible -- and reproducible.

Using the best available computer graphical software tools (1991-1993), D.C. Coy in his dissertation developed a reproducible method to create Gibbs' surfaces for actual (to scale) materials, Ref.[6]. Unfortunately because computer graphics is a new fast evolving technology, the graphic software Application Programming Interface (API - an interface programmers use to build applications) used by Coy no longer works on current computer operating systems. However Coy carefully outlined the development of the surfaces for actual materials which can be revived using current graphical APIs. To avoid a similar situation in the future it is recommended that future diagrams be created using a ISO standard format, e.g. VRML-2 or X3D. These standard file formats can be loaded into future graphical software APIs as they evolve with the demands of ever changing graphic hardware and operating systems. This should extend the usefullness of diagrams over time, however this will inevitably change as well. To archive results for future applications it is recommended to store a list (ASCII human readable text format) of point-coordinates (vertices) that define points on the energy-entropy-volume surface and the corresponding list of polygons (connectivity) that connect vertices into polygon shapes. A list of colors assigned to vertices and polygons can also be used to map properties, e.g. pressure and temperature, onto the energy-entropy-volume surface. These archived ASCII text file lists will not change with ever changing graphic software APIs. Using this archived format only minimal changes will be necessary to reconstruct Gibbs' surfaces 134 years from now.

Specialized computer graphical programs were developed by Coy to extend Gibbs' graphical method to include Legendre transformations in Dr. Coy's dissertation, "Visualizing thermodynamic stability and phase-equilibrium through computer graphics", Ref.[6]. After 120 years Dr. Coy and his professor Ken Jolls were the first to provide a detailed explanation on how to calculate and create Gibbs' surfaces to scale and created a web site that exemplifies how others can share in this insightful experience. Except for Coy and Jolls effort in 1993 little has been done to promote the graphical method. Instead analytic methods based on Gibbs equation of state have been developed over the last 134 years. As insightful as the graphical methods described by Gibbs and Maxwell may be, students have not been taught to think visually, at least in the context of science and math. This is what Dr. Coy describes as Gibbs' geometric thinking. Unfortuantely 134 years of momentum has been devoted to developing analytic methods. Perhaps we have become analytically QWERTY (comtemporary computer keyboard configuration) even though we are aware there are more efficient keyboards and graphical methods that can be more insightful. With this observation the challenge and opportunity exists to teach analytic and graphical methods together and show that both methods complement each other. This can be accomplished when graphical methods are first developed in a general sense and then applied to a specific problem. At the end of his first publication Gibbs supported the idea of developing a general graphical method independent of the application or graphical tools, "Such a course would have been better fitted to show the independence and sufficiency of a graphical method, ....", pg. 342 Ref.[1]. Perhaps the lack of graphical tools in 1873 encouraged geometric thinking.

Independent of using a specific graphical tool, a general graphical method (" ... coextensive in their applications ... ") was developed above as a surface in Fig. 5, that can be used to describe Gibbs' equation of state. The objective here is to combine the graphical and analytic methods to facilitate an understanding of the relationship between the various thermodynamic state variables.

Figure 8. Gibbs' energy function of entropy and volume. Coefficients highlighted green and blue show
the connection   to the components of the vector gradient of the energy function.   The final equation is
known as Gibbs equation of state. This equation is the total differential of the energy function.                

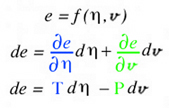
According to the general graphical method developed to envision total differentials, all five thermodynamic state variables (e, η, v, T, P), related in the equation of state above, coexist at any arbitrary point A, at x=x₁ y=y₁ in Fig. 5. Hence any point on the energy-entropy-volume surface uniquely describes a thermodynamic state. In Gibbs equation of state the vector components of a gradient of the scalar energy function are the definitions for temperature and pressure. Hence lines of constant temperature and pressure can be mapped as a collection of connected points on the curved surface with the same slopes where the surface is defined by the scalar two-dimensional function of energy as a function of entropy and volume. This is why Maxwell could use the sun's "grazing" rays to identify points on the surface with similar slopes. The vector components of the gradient that define the slopes of the tangent plane are highlighted using green and blue colors. Maxwell also used color to highlight lines of constant pressure and temperature scribed onto his sculptured surface, which has since faded in Fig. 2 but reconstructed in Fig. 6. In Coy's dissertation this tangent plane was drawn in special cases to understand properties of interest. Using the graphical method for envisioning total differentials, a glyph representing the total differentials also uses the idea of a tangent plane to show the pressure, temperature, position vector, and the corresponding total differential. This glyph could be drawn interactively in a highlighted window next to the surface as the mouse pointer moves from point to point (A to B) along the scalar two-dimensional function energy-entropy-volume surface. If the mouse pointer is static then no glyph is drawn. This is an essential requirement because the total differential only exists with respect to a position vector that defines two points A and B. From a thermodynamic view point this corresponds to the underlying question when working with thermodynamic theory of state, that is, what thermodynamic processes exist when moving from point to point along the energy-entropy-volume surface. Using this idea Maxwell demonstrated how to determine whether a substance, composed of a mixture of different states that coexist at points A and B, e.g. solid, liquid, or gas (triple point), "will tend of itself to pass from one of these states to the other". This is determined by the amount of energy freely available (Gibbs' free Energy) which is associated with the curvature of the "primitive" surface and orientation of the triple point tangent plane which Gibbs labels as the "dissipated energy surface". Maxwell lists triple point thermodynamic processes associated with Gibbs' free energy next to fig.26d on page 206 of Ref.[2]. Hence implementation of the glyph at points A and B would first require an understanding of the underlying thermodynamic concepts associated with the list on page 206 of Ref[2].

Figure 9. Total differential glyph for any arbitrary scalar function of two independent
variables ( x, y ).   NOTE:   Points A and B must be defined if glyph is to be drawn. 

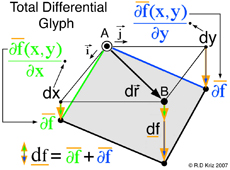
Here the scalar function, f(x,y), is Gibbs energy, e(η,v), that is a function of entropy, η, and volume, v. The gradient terms highlighted in green and blue are themselves thermodynamic state variables: temperature, T, and negative pressure, -P. It is fortunate that the gradient terms are additional thermodynamic state variables that coexist at point A along with energy, entropy and volume. Regardless if the gradient terms highlighted with green and blue colors are additional properties or not, the total differential can always be calculated and envisioned using the glyph. In this case the total differential is a differential change of energy, de, associated with moving from point A to point B on the energy-entropy-volume diagram.

It is now possible to explore other total differential equations that could be used to understand different complex scientific phenomena. This requires that the two-dimensional function be plotted as a raised curved surface where the idea of a total differential glyph can be invoked. Because of the availability of popular computer graphic tools, two-dimensional functions are readily plotted as raised curved surfaces simply because "it looks interesting". With these raised surface plots, there is now a conceptual link to the total differential and the same visual thinking first implemented by Gibbs and Maxwell can be realized coextensive to its application, that is, if the user appreciates the significance of a total differential and its associated properties. Other concepts related to the total differential can be explored. For example the idea of the comoving derivative (total derivative with respect to time), used in continuum mechanics, is an extension of the total differential in the same sense that the idea of the total differential is an extension of the gradient. Similarly other examples will come to mind depending on the experience of the scientist. Create the graphical method -- discover, or in this case, create the science. How to design the tools follow. For Maxwell it was clay and plaster. Unfortunately because of the wide-spread use of computers and "easy-to-use" graphical software, we are tool rich but methodology poor. This emphasis on just using existing tools without visual thinking does not encourage scientists to develop new graphical methods.

Summary

The development of the thermodynamic theory of state is a rare but excellent example that demonstrates how scientists combine analytic and graphical methods together with how they understand science. How scientists combine analytical and graphical models into new knowledge exemplifies a cognitive processes that includes visual thinking or what Dr. Coy describes as "geometric reasoning", Ref.[6]. This new knowledge was reported and documented by Gibbs as a graphical method, so that others could reproduce and build on that understanding. As the graphical method was being developed by Gibbs the intent was not to use graphics for presentation but rather to develop the theory. This is contrary to the popular belief that imaging in science is used for presentation which can at times be insightful. For example if scientists do experience any insight when working with diagrams or imaging, this experience is understood to be unique to the researcher as a subjective experience, which may have educational value by reporting this experience as a scientific visual thinking anecdote: a short tale narrating an interesting or amusing biographical incident that may be useful for educational or outreach purposes to the general public who do not understand the science. At best the result becomes an intriguing picture on a stamp or the cover of a scientific text book. After reading and STUDYING Gibbs and Maxwell, perhaps the reader would agree that neither Gibbs nor Maxwell developed their graphical method for presentation, a metaphor, or as an intriguing ancetodal experience that could not be scientifically reproduced. Rather the graphical method was sufficiently developed and described by Gibbs to be inclusive with developing the thermodynamic theory of state, which was reproduced and further developed graphically by Maxwell. Recall in summary Gibbs states,

"In the foregoing discussion, the equations which express the fundamental principles of thermodynamics in an analytical form have been assumed, and the aim has only been to show how the same relations may be expressed geometrically. It would, however, be easy, starting from the first and second laws of thermodynamics as usually enunciated, to arrive at the same results without the aid of analytical formulae, to arrive, for example, at the conception of energy, of entropy, of absolute temperature, in the construction of the diagram without the analytical definitions of these quantities, and to obtain the various properties of the diagram without the analytical expression of the thermodynamic properties which they involve."

"Such a course would have been better fitted to show the independence and sufficiency of a graphical method, but perhaps less suitable for an examination of the comparative advantages or disadvantages of different graphical methods."

References:

1. J.W. Gibbs, Part 1,"Graphical Methods in the Thermodynamics of Fluids" and Part 2, "A Method of Geometrical Representation of the Thermodynamic Properties of Substances by Means of Surfaces", Transactions of the Connecticut Academy, Vol. II, Part 1, pp. 309-342 and Part 2, pp. 382-404", 1873.
   
2. J. Clerk Maxwell, Theory of Heat, Longmans, Green, and Co, pp. 195-208, 1904.
   
3. The Scientific Letters and Papers of James Clerk Maxwell, Vol. III, 1874-1879, Edited by P.M. Harman, Cambridge University Press, 2002.
   
4. W.P. Boynton, "Gibbs' Thermodynamic Model", Phys. Rev., Series 1, Vol.10, pp. 228-233, 1900.
5. Maxwell on heat and statistical mechanics: on "avoiding all personal enquiries" of molecules, edited by E. Gaber, S.G. Brush, and C.W.F. Everitt, Lehigh University Press, pp. 49-50, 1995.
6. Daniel Charles Coy, "Visualizing thermodynamic stability and phase-equilibrium through computer graphics", Ph.D. dissertation, Iowa State University, 1993.